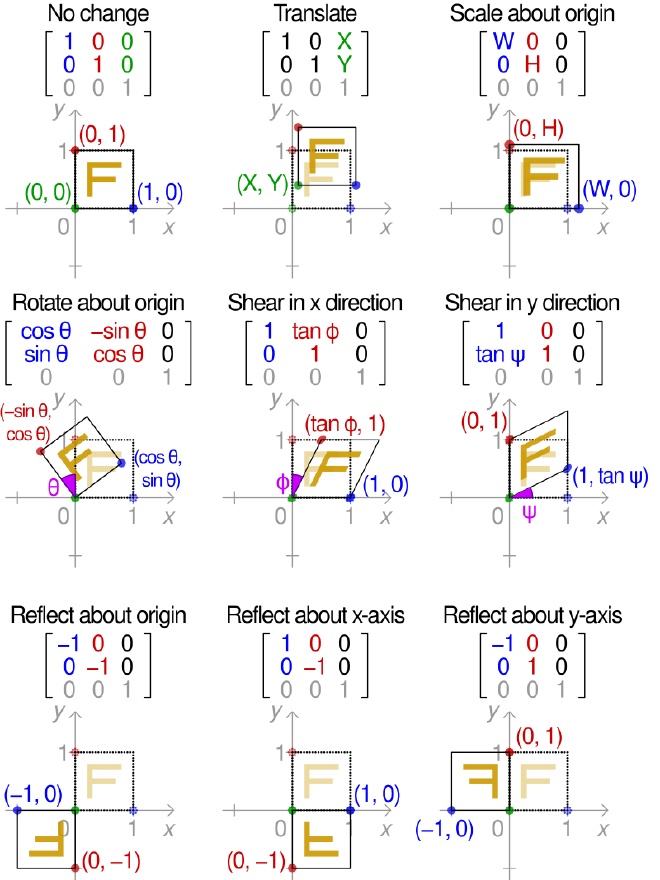
Affine Transformation

Definition #

An affine transformation is a geometric transformation that preserves:

• Collinearity (points on a line remain on a line after transformation)
• Ratios of distances (the midpoint of a line segment remains the midpoint after transformation)
• But not necessarily Euclidean distances and angles

Types of Affine Transformations: #

1. Translation: Shifting the object by a constant distance in the x- and y- directions.
2. Scaling: Changing the size of an object by a factor along each axis.
3. Rotation: Rotating the object around the origin by an angle θ.
4. Shearing: Distorting the object along one axis.
5. Reflection: Reflecting the object about an axis.

Equation: #

Affine transformations can be expressed in a single matrix multiplications

$$ \begin{bmatrix} x’ \\ y’ \\ 1 \\ \end{bmatrix} = \begin{bmatrix} a & b & t_{x} \\ c & d & t_{y} \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} $$